Učitelka nevynese za celou hodinu ani jednu pravdu, zato položí desítky otázek. Děti ve vášnivých diskusích, a to nejen nad obsahem trojúhelníku, ale i o vzájemných vztazích. Tak vypadaly dvě hodiny Hejného matematiky na Fakultní základní škole na pražském Barrandově.
Na parkovišti stojí jedna dvanáctina kamionů, jedna šestina autobusů, polovina aut a čtvrtina motorek. Kolik je kterých, když víme, že aut je dvanáct? zadává učitelka Sandra Holáková první příklad. I já zapínám mozkové závity, ale než se doberu výsledků, pár dětí už se hlásí. Pro čtvrťáky nic těžkého, příklad na rozcvičení. Zlomkům už se věnují nějakou dobu, i když to tak třeba ani nenazývají. Pro Hejného metodu nejsou důležité pojmy a poučky, jde o to prostě přemýšlet a objevovat vlastní řešení.
Děti sedí ve skupinkách zhruba po čtyřech. Jde o týmy dlouhodobé, které se občas přeskládají, aby získaly jinou dynamiku. Při matematice podle Hejného, která je na spolupráci dětí založená, je to důležité. Chvíli přemýšlí každý sám, ale gró práce je v tom, že skupinka probírá nápady na řešení příkladu společně. Učitel musí hlídat dobré fungování týmů, aby se každý dostal ke slovu a aby se ti, kteří mají jiné talenty než matematické, pouze „nevezli“.
„Můžete začít sdílet, jaká řešení se objevila,“ startuje Sandra Holáková druhou fázi práce. „Jaká myšlenka byla první? Myslíš, Aničko, že Kuba to udělal podobně jako ty?“ povzbuzuje děti dalšími otázkami. Teprve potom přijde výzva, kdo chce jít k tabuli a svůj způsob řešení představit ostatním.
Počítej pomalu
„Šel na to někdo jinak?“ ptá se učitelka, když jeden z chlapců odprezentuje, jak došel k výsledku. „My jsme to řešili v koláči,“ zaznívá z jiné skupinky. Žádné řešení se nevydává za jediné správné, vždycky je možnost udělat vlastní objev. „Teď máte minutku na to si ve skupině říct, co vás tam překvapilo, co jste pro sebe objevili,“ zakončuje učitelka.
Mezitím prochází mezi skupinami a otázkami směruje práci ve skupinách. „Nyní se vrátíme k úloze ze včerejška, na kterou jsme si dali čas, abychom ji promysleli.“ Rychlost se v Hejného matematice nenosí, důležitější než počet spočítaných příkladů je věci opravdu dobře promyslet. „Jen to, na co si počtář přijde sám a čemu opravdu porozumí, dokáže prohloubit jeho matematické myšlení a bude mu k užitku i příště,“ říká Sandra Holáková.
Učitelka třikrát zatleská a položí si ruku na ústa. Znamená to, že by chtěla, aby byla pozornost obrácena k ní. Děti k ní zvedají hlavy a některé ji v gestu napodobí. Přichází čas zreflektovat práci ve skupinách. V každé z nich má někdo roli „pozorovatele“, který má za úkol sledovat, jak se kdo zapojuje. Někdo jiný zas funguje jako „hlídač půlmetrového hlasu“ neboli snesitelné hladiny hluku. Podstatné úlohy tedy mají i ti, kteří nejsou zrovna nejsilnější v matematice. „Verčo, co ty si o tom myslíš,“ snaží se učitelka vtáhnout do hry i ty, kteří vypadají, že jsou mimo.
Zasloužený potlesk
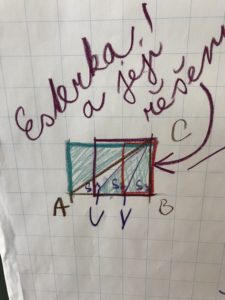
Mário tvrdí, že všechny trojúhelníky mají stejný obsah. Je to pravda? zní zadání další úlohy. Průběh se opakuje: děti přemýšlejí nejdřív každý sám, potom ve skupině. Nakonec jde jeden z chlapců k tabuli, aby představil svoje řešení. Je vidět, že je mu všechno jasné, ale vysvětlit to ostatním se mu nedaří. Děti nejsou spokojené, zdá se jim, že „začíná odprostředka“ a volají na něj spoustu připomínek.
Ester, která jde po něm, odprezentuje svůj způsob řešení krok po kroku. Vysekne způsob výpočtu obsahu trojúhelníku jako z učebnice. „Opravdu na to přišla sama? Vy jste nikdy ve třídě neřekla, jak se obsah trojúhelníku počítá?“ kladu později podezřívavé otázky. „Nikdy neříkám žádné řešení. Děti opravdu dokážou úplně na všechno přijít samy. Hejného metoda je detailně promyšlená a probíhá v jakési spirále, takže se postupně buduje kvalita myšlení a děti jsou schopné přicházet na složitější a složitější objevy. Jen se jim musí nechat prostor,“ vysvětluje Sandra Holáková.
Když Ester skončí svou prezentaci, děti jí zatleskají. „Protože přišla opravdu s důkazem,“ vysvětluje mi později učitelka. „Děti vědí, že pouhý výsledek nestačí. Obohacující je, když někdo umí vysvětlit, jak k výsledku došel a tím ‚postrčí‘ myšlení ostatních.“
V nepříjemné atmosféře se nic nevymyslí
Mezitím zvoní na přestávku, ale jediný, kdo se tím vzrušuje, jsem já. Děti jsou evidentně zvyklé práci dokončit. V tom se ozve školní rozhlas: „Školník Šídlo vysílá…“. V půlce věty začne zvuk přeskakovat, školníku Šídlovi nebylo dáno dokončit myšlenku. Děti se smějí. „Jak byste se cítili vy, kdybyste chtěli někomu něco sdělit a selhala by vám technika,“ apeluje učitelka na empatii.

Jeden velký matematický objev se dnes podařil, není tedy problém věnovat čas osobnostně-sociální výchově, která je nedílnou součástí Hejného metody. Velká příležitost k tomu přichází ke konci druhé hodiny. V tu chvíli se pracuje ve skupinách, které vznikly losem. Jeden z chlapců si stěžuje, že se mu dívky z jeho skupiny smějí, že je mezi nimi jediný a že s nimi bude mít peklo. Holky se brání, že slovo peklo se vztahovalo k obtížnosti úlohy, Tadeáš nevěří. Matematická práce se přerušuje, učitelka všechny žádá, aby si sedli do kruhu. „Potřebuju, abyste si teď všichni viděli do tváře.“ Stejně jako v matematice, i v mezilidských vztazích jsou hlavní „zbraní“ učitele otázky.
„Každému se může stát, že se dostane do skupiny, kde to pro něj bude velká výzva. A kdykoli v životě se může stát, že mám pocit, že se mi někdo vysmívá. Co můžeme v takové situaci dělat?“ Zeptat se, jak to myslel, říct neurážej mě, nebo mně to vadí, navrhují děti. „Měl hned říct, že mu to vadí, a my bychom mu vysvětlily, že jsme to nemyslely na něj,“ brání se jedno z děvčat. „Dalo se to z jeho výrazu poznat, že se ho to dotýká?“ připomíná učitelka, že být empatický znamená všímat si i věcí, které nejsou vyřčeny.
Strážci spravedlnosti
Všichni se zapojují, každý k tomu má co říct. Překvapuje mě, že i kluci, o kterých se přece říká, že se neradi patlají ve vztazích. „Každý z nich už v podobné situaci někdy byl, takže vnímají, že je důležité si to vyjasnit,“ vysvětluje mi později Sandra Holáková a dodává, že v tomhle věku jsou děti velkými strážci spravedlnosti. Dokud se nevyřeší konflikt, nemá podle ní smysl se snažit o něco v matematice. „Ve třídě musí být příjemné emoce a bezpečné prostředí. Jinak nelze rozvíjet kognitivní stránku.“
Důležité ale také je nepatlat se v konfliktech moc dlouho. „Když řešíme vztahové problémy, všichni se zapojí – tys mi…, a já jsem ti… – a narůstá to ve spirále a původní pravda už je nedohledatelná. Je potřeba hledat konstruktivní způsob, jak konflikty řešit. I já se to stále učím,“ říká Sandra Holáková, která učí teprve sedmým rokem, ale už teď ji profesor Milan Hejný doporučuje jako někoho, kdo jeho metodu aplikuje dobře.
Více čtěte v rozhovoru s učitelkou Sandrou Holákovou.
DOPORUČENÉ ČLÁNKY
21. 08. 2022 Bára Procházková Pět věcí, které budou v novém školním roce jinak
28. 02. 2023 Lucie Rybová Život celé rodiny se zúžil na domácí úkoly, podle právníků jsou navíc nezákonné




Má pocit, že další reklamní článek na Hejného metodu je na světě. Když jsem se zajímala o ZŠ Barrandov a výuku matematiky na ní, bylo mi odpovězeno, že zhruba v každém ročníku jsou tři třídy, v jedné se vyučuje Hejného metoda a ve zbylých dvou „normální“ matematika s prvky Hejného, že ze zkušeností s Hejného metodou zjistili, že není vhodná pro všechny a že si rodiče při nástupu do první třídy mohou vybrat, v jaké chtějí být zařazeni třídě. Tento článek mne velmi irituje, protože působí dojmem, že Hejného metodě není co vytknout. Opak je pravdou. Na což poukazuje spousta jiných článků na internetu a v tisku.
dobrý den, co to znamená „reklamní článek“? Prostě jsem na ZŠ Barrandov strávila dvě hodiny a popsala své dojmy, myslím, že docela věcně; názor, ať si každý udělá sám. Nic k vytknutí jsem opravdu nenašla, naopak jsem si říkala, jak by to asi bylo s mou nenávistí k matematice, kdybych měla možnost učit se ji takhle. A jací dospělí vyrostou z dětí, o jejichž pocity se – na rozdíl od mojí generace – ve škole někdo zajímá, učí je vyjadřovat, a vycházet a spolupracovat s ostatními.
S tou vhodností nikoli pro všechny máte ovšem pravdu, p. prof. Hejný opakovaně apeluje na to, aby žádní učitelé nebyli k výuce jeho metodou nuceni, a svoboda výběru pro rodiče (potažmo děti) by se mu asi taky líbila. Pak je ale mnoho učitelů, kteří se v Hejného metodě – tak jako Sandra Holáková – doslova našli. Více o tom pohovoří v rozhovoru, který uveřejníme ve čtvrtek. Děkujeme za komentář.
Dobrý den, děkuji za reakci, já také píši jen svůj názor. Tím reklamním článkem bylo myšleno to, že někteří lidé si názor sami vytvoří mylný podle líbivě podané reportáže a mohli by si snad myslet, že takto probíhající hodina je po všech stránkách ok. Jenže mně tak nějak vychází, že žáci spočítali za dvě hodiny asi dva příklady a k tomu si nejsem jistá, zda jste psala o hodinách matematiky či spíš občanské či rodinné výchovy. Rozhodně jsem pro komunikaci ve škole, řešení problémů atd., ale patří toto do hodiny matematiky?! „Počítej pomalu“ – nezlobte se, v práci jsou na mne kladeny takové nároky, že s tímto heslem, bych si nevydělala ani na chleba, stejně tak nemůžu v práci očekávat potlesk. Ano pan Hejný apeluje na to, aby se metoda nezaváděla nucením, ale jsou jiní, kteří ji nutí místo něj. Snad v každé diskuzi narazíme na konstatování: náš učitel k tomu byl donucen, byl donucen a po dvou letech přešel na jinou školu, náš učitel to učí a špatně, protože naše dětí neumí počítat, náš učitel to nedává, učí to tak nějak napůl apod.
Můžu Vás uklidnit, dva příklady nespočítali, to jen do reportáže se nevejde všechno, pak by vás to nebavilo číst. Myslím, že sociální a komunikační dovednosti a schopnost spolupráce jsou tak zásadní, že je žádoucí rozvíjet je v každém předmětu. Patří totiž mezi „klíčové kompetence“ a od započetí tzv. kurikulární reformy v roce 2004 jsou součástí rámcového vzdělávacího programu pro ZŠ jako něco, co by mělo být integrováno do každého předmětu a patřit mezi jeho výstupy. Hejného metoda tedy v důsledku není bůhvíjaká alternativa, prostě jen naplňuje 14 let (!) starý „výmysl“ ministerstva školství.
100% – reklama. S HM matematiku umět nebudete. Budete umět HM. Někteří s matematikou nemají problém a potřebuji ji na VŠ. Ale když škola plošné zavadí HM , musí brat doučovaní?
Jestliže to ta zš opravdu dělá takhle,tak tomu přece nelze nic vytknout.Naopak.Mohou si vybrat jak učitelé,tak rodiče.A tak je to dobře.A věřte mě,kdyby si mohly vybrat děti,vybraly by si Hejného
Jestli něco velmi oceňuji na p. učitelce, tak schopnost řešit konstruktivně vztahy mezi dětmi. Pokud jsou takto vedeny od začátku, je to velmi ku prospěchu celé třídě. Není nic horšího, než učitel, který má pocit, že děti si vše vyřeší samy, že rozdá jen poznámky nebo tresty a nic ho nezajímá a tváří se, že v jeho třídě je vše ok. S postupem času pak problémy jen narůstají a je zaděláno na šikanu a pokřivené vztahy mezi dětmi.
Dobrý den, mám jiný názor. Jsou děti, které jsou v Hejného třídách nespokojené a jen opravdová matematika jim chybí. Chtějí počítat to, co jejich starší sourozenec třeba na gymnáziu, kde tato metoda není. Připadá jim dětinské používat zvířátka, krokovat. Vadí jim hluk a malá míra organizovanosti během hodiny.
Proč tedy tolik žáků letos propadlo u maturity z matiky a další shodný počet z ní měl za4?
Nevidím, že by Vaše otázka měla něco společného s článkem a diskuzí pod něm. A odpovědět na otázku neznám. Myslím si ale, že důvodem může být to, že velké procento žáků, které nedovedu ani odhadnout (40%?), na středních školách vůbec nemá být, plus celé nastavení školství a přistup k životu v nynější společnosti. Myslím si, že do revoluce 1989 byly výsledky ve školství lepší a od té doby to v mnoha směrech upadá. Ale to je jen můj názor.
Vaše důvody mají samozřejmě také své opdstatnění.Já jsem tím chtěla říct,že v podstatě polovina žáků,kteří letos dobrovolně zvolili u maturity matematiku,se za 13 let studia asi moc nenaučili.Tedy,že už na zš je s vyučováním matiky problém.Je potřeba hledat cesty,jak to zlepšit.
Také rozumím, že vy to asi vidíte tak, že možnou cestou je změna přístupu k výuce a použití nových metod. Osobně bych spíše volila cestu přísnějšího síta před středními školami a tím by nám zbylo již jen pár dětí v každé třídě, které by maturitu z matematiky nezvládlo … a na ty bych – přeženu to – použila bič. Nevím, nevím, jestli se to v naší zemi ubírá správným směrem. Připadá mi, že chyba je často již na začátku v nefungující rodině, ve špatných hodnotách ve společnosti, v nekvalitních učitelích, ale přes toto všechno se domnívám, že není nutné dělat z matematiky tělocvik, výtvarku, diskuzní kroužek, rodinnou výchovu. Do jisté míry samozřejmě ano, ale stále v předmětu matematika musí být znalost matematiky na prvním místě.
Je možné, že to některým dětem může připadat dětinské, ale vede to k velmi dobrému pochopení problematiky. Velké množství dětí v páté třídě matematické úkony pouze umí nazpamět, bez hlubšího pochopení. Když řeknu, že je to průměrně polovina třídy, jsem ještě velký optimista. To je přesně důvod, proč pak u maturity tolik dětí neuspěje. Opravdová matematika je ta, kterou děti chápou. Kritizujete i to, že někteří učitelé jsou k Hejného metodě donuceni – stejně tak obrovské množství učitelů je nuceno učit zastaralými metodami typu a není jim umožněno učit alternativně – tak to prostě je. Když mi to nevyhovuje, změním školu. PS: Zastaralými metodami myslím např. toto: Vysvětlím látku, děti zapíší do sešitu, naučí se zpaměti, spočítáme 30 příkladů, napíšem test, jede se dál. V hodině je ticho, klid, nikdo se na nic neptá, nikdo nedebatuje, nezpochybňuje, inteligentní to chápou, méně inteligentním to dovysvětlí doma rodiče, čtvrtině třídy je to úplně putna, ale když se učitel po svém dlouhém výkladu zeptá: Kdo to nechápe?, nikdo se nehlásí, protože nikdo z těch nechápajících v tu chvíli nemá žádný zájem a žádnou motivaci to pochopit.
Máte pravdu, paní Lucie, další reklamní článek je na světě. To, že Hejného metoda není vhodná pro všechny, respektive je vhodná jen pro matematicky nadané, je vidět i z tohoto článku. Cituji: „V každé z nich má někdo roli „pozorovatele“, který má za úkol sledovat, jak se kdo zapojuje. Někdo jiný zas funguje jako „hlídač půlmetrového hlasu“ neboli snesitelné hladiny hluku. Podstatné úlohy tedy mají i ti, kteří nejsou zrovna nejsilnější v matematice. “ Tady je vidět, že ti „slabší“ vůbec matematiku (ani dle Hejného ani klasickou) nedělají – ale jedničku za příklad dostanou všichni. Ti slabší se prostě hodí přes palubu – a jak jde čas a zvětšuje se náročnost příkladů, padá jich přes palubu víc a víc….
100% – reklama. S HM matematiku umět nebudete. Budete umět HM. Někteří s matematikou nemají problém a potřebuji ji na VŠ. Ale když škola plošné zavadí HM , musí brat doučovaní?
Když jsem se snažil někde zjistit, v čem spočívá Hejného metoda, nepodařilo se mi to. Nikde jsem nic nenašel.
A mám k tomu ještě jednu poznámku: Úloha „Na parkovišti stojí jedna dvanáctina kamionů, jedna šestina autobusů, polovina aut a čtvrtina motorek. Kolik je kterých, když víme, že aut je dvanáct?“ není jednoznačně řešitelná. Když víme, že aut je 12 a stojí tam polovina aut, stojí tam tedy 6 aut – ale o autobusech, kamiónech a motorkách žádnou další informaci nemáme. Protože máme jednu rovnici o 5 neznámých:
1/12 k + 1/6 b + 1/2 a + 1/4 m = C
a dodatkovou informaci a = 12. Taková úloha vede na 4parametrický systém. A rozhodně to není úloha pro 4. třídu ZŠ.
Dobrý den, spočítali jsme to takto: kamiony 2, autobusy 4, motorky 6, auta 12.